NMR physics

Today, I reviewed the basic knowledge of NMR so that I would be able to find the proper predictors of it.

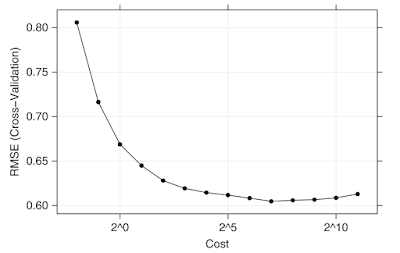
Summary

Data selection

No diaelectric data because they are also very expensive.

Try to use GR, neutron, sonic, density, resistivity data to predict NMR.

NMR:

NMR porosity is independent of matrix minerals, and the total response is very sensitive to fluid properties. Differences in relaxation times and/or fluid diffusivity allow NMR data to be used to differentiate clay-bound water, capillary-bound water, movable water, gas, light oil, and viscous oils. NMR-log data also provide information concerning pore size, permeability, hydrocarbon properties, vugs, fractures, and grain size.

T1: the longitudinal relaxation time.

T2: the transverse or spin-spin relaxation.

The decay or relaxation time of the NMR signals (T2) is directly related to the pore size. The NMR signal detected from a fluid-bearing rock therefore contains T2 components from every different pore size in the measured volume. Using a mathematical process known as inversion, these components can be extracted from the total NMR signal to form a T2 spectrum or T2 distribution, which is effectively a pore size distribution.

The so-called ‘T2 cut-off’ in a T2 distribution is the T2 value that divides the small pores that are unlikely to be producible from the larger pores that are likely to contain free fluid. The integral of the distribution above the T2 cut-off is a measure of the free fluid (mobile fluid) in the rock.  The portion of the curve below the cut-off is known as bound fluid and is made up of the clay bound fluid and the capillary bound fluid.

Tomorrow, I will continue to learn more about NMR and try to find the proper predictors.

Chapter 7 application (7.3&7.4)

Today, I finished Chapter 7 (7.3&7.4) and found something useful for my research.

Summary

SVM: Support Vector Machines

SVMs are a class of powerful, highly flexible modeling techniques.

The SVM regression coefficients minimize

There are several aspects of this equation worth pointing out. First, the use of the cost value effectively regularizes the model to help alleviate the over-parameterized problem. Second, the individual training set data points are required for new predictions. Only a subset of training set data points where , are needed for prediction. Since the regression line is determined using these samples, they are called the support vectors as they support the regression line. Which kernel function should be used? This depends on the problem. Note that some of the kernel functions have extra parameters. These parameters, along with the cost value, constitute the tuning parameters for the model.

K-Nearest Neighbors

Two commonly noted problems are computational time and the disconnect between local structure and the predictive ability of KNN.

Next week, I will continue to read the book and try to finish it before the holiday.

Chapter 7 application (7.2)

Today, I read Chapter 7 (7.2) and find something useful for my research.

Summary

MARS: Multivariate Adaptive Regression Splines

GCV: generalized cross-validation

There are two tuning parameters associated with the MARS model: the degree of the features that are added to the model and the number of retained terms. The latter parameter can be automatically determined using the default pruning procedure (using GCV), set by the user or determined using an external resampling technique.

There are several advantages to using MARS. First, the model automatically conducts feature selection; the model equation is independent of predictor variables that are not involved with any of the final model features. This point cannot be underrated. Given a large number of predictors seen in many problem domains, MARS potentially thins the predictor set using the same algorithm that builds the model. In this way, the feature selection routine has a direct connection to functional performance. The second advantage is interpretability. Each hinge feature is responsible for modeling a specific region in the predictor space using a (piecewise) linear model. When the MARS model is additive, the contribution of each predictor can be isolated without the need to consider the others. This can be used to provide clear interpretations of how each predictor relates to the outcome. For nonadditive models, the interpretive power of the model is not reduced. Finally, the MARS model requires very little pre-processing of the data; data transformations and the filtering of predictors are not needed.

Another method to help understand the nature of how the predictors affect the model is to quantify their importance to the model. For MARS, one technique for doing this is to track the reduction in the root mean squared error (as measured using the GCV statistic) that occurs when adding a particular feature to the model.

The following figure compares the predictors and we can see the importance of predictors from the figure.

Tomorrow, I will continue to read the book.

Chapter 7 application (7.1)

Today, I read Chapter 7 (7.1) to find something useful for my research.

Summary

Nonlinear Regression Models

Neural Networks

Weight decay is an approach to moderate over-fitting. It is a penalization method to regularize the model similar to ridge regression.

As the regularization value λ increases, the fitted model becomes more smooth and less likely to over-fit the training set.

Of course, the value of this parameter must be specified and, along with the number of hidden units, is a tuning parameter for the model. Reasonable values of λ range between 0 and 0.1. Also note that since the regression coefficients are being summed, they should be on the same scale; hence the predictors should
be centered and scaled prior to modeling.

Neural networks are models which are more accurate than linear models. It can be used to be applied to the log data. After building the data matrix, we may have dozens of predictors, namely log data to predict outcomes, namely NMR data. Before building the model , we can first center and scale predictors and use PCA to decrease correlations between every pair of predictors. Then we can set a set of tuning parameters of weight decay and number of hidden units to build the model. After running the codes, we can find the optimized tuning parameter so that  we can choose the optimized neural network model. It may perform well in predicting NMR data.

If we can just find the local optimization but not the global one, we can use the model averaged neural networks to solve the problem. The approach is that we start do modeling with several different starting numbers so that we can get different results of the model. Then we average them to get the more reliable results.

The following is an example of the comparison of neural networks with different tuning parameters.

Tomorrow, I will continue to read the book.

Chapter 6 Application (6.4&6.5)

Today, I finished reading Chapter 6 to find something useful for my research.

Summary

Because the dimension reduction offered by PLS is supervised by the response, it is more quickly steered towards the underlying relationship between the predictors and the response.

NIPALS: nonlinear iterative partial least squares algorithm

The constructs of NIPALS could be obtained by working with a “kernel” matrix of dimension P × P, the covariance matrix of the predictors (also of dimension P×P), and the covariance matrix of the predictors and response (of dimension P ×1). This adjustment improved the speed of the algorithm, especially as the number of observations became much larger than the number of predictors.

SIMPLS: simple modification of the PLS algorithm.

If a more intricate relationship between predictors and response exists, then we suggest employing one
of the other techniques rather than trying to improve the performance of PLS through this type of augmentation.

Partial least square regression vs. Ordinary least square regression

Penalized models

Combatting collinearity by using biased models may result in regression models where the overall MSE
is competitive.

One method of creating biased regression models is to add a penalty to the sum of the squared errors.

Ridge regression adds a penalty on the sum of the squared regression parameters:

Penalty increase, bias increase, variance decrease, model under-fit.

Lasso: least absolute shrinkage and selection operator model

A generalization of the lasso model is the elastic net. This model combines the two types of penalties:

The advantage of this model is that it enables effective regularization via the ridge-type penalty with the feature selection quality of the lasso penalty.

Tomorrow, I will continue to read Chapter 7 of the book.

Review of Codes

Today, I review the codes of the book from Chapter 3 to Chapter 5.

I think that I forget some of the codes when I read the book, so I decide to spend some time reviewing them.

Summary

#Coefficient of determination (R^2): the proportion of the information in the data that is explained by the model.
#It is a measure of correlation, not accuracy. It is dependent on the variation in the outcome. Same RMSE, larger variance, larger R^2.
observed=c(0.22, 0.83, -0.12, 0.89, -0.23, -1.30, -0.15, -1.4, 0.62, 0.99, -0.18, 0.32, 0.34,
           -0.3, 0.04, -0.87, 0.55, -1.3, -1.15, 0.2)
predicted=c(0.24, 0.78, -0.66, 0.53, 0.7, -0.75, -0.41, -0.43, 0.49, 0.79, -1.19, 0.06, 0.75,
           -0.07, 0.43, -0.42, -0.25, -0.64, -1.26, -0.07)
#in practice, the vector of predictions would be produced by the model function
residualvalues=observed-predicted
residualvalues
summary(residualvalues)
axisrange=extendrange(c(observed, predicted))
plot(observed, predicted, ylim=axisrange, xlim=axisrange)
abline(0, 1, col="darkgrey", lty=2)
plot(predicted, residualvalues, ylab = "residual")
abline(h=0, col="darkgrey", lty=2)
library(caret)
R2(predicted, observed)
RMSE(predicted, observed)
cor(predicted, observed)
cor(predicted, observed, method = "spearman")

library(AppliedPredictiveModeling)
data(twoClassData)
str(predictors)
str(classes)
set.seed(1)
library(caret)
trainingrows=createDataPartition(classes, p=0.8, list=FALSE)
head(trainingrows)
trainpredictors=predictors[trainingrows, ]
trainclasses=classes[trainingrows]
testpredictors=predictors[-trainingrows, ]
testclasses=classes[-trainingrows]
trainpredictors
trainclasses
testpredictors
testclasses
#maxdissim
#resampling
set.seed(1)
repeatedsplits=createDataPartition(trainclasses, p=0.8, time=3)
str(repeatedsplits)
#to create indicators for 10-fold cross-validation
set.seed(1)
cvsplits=createFolds(trainclasses, k=10, returnTrain = TRUE)
str(cvsplits)
fold1=cvsplits[[1]]
cvpredictors1=trainpredictors[fold1,]
cvclasses1=trainclasses[fold1]
nrow(trainpredictors)

nrow(cvpredictors1)

#e1071package contains the tune function
#errorest function in the ipred package
#the train function in the caret package
library(caret)
library(AppliedPredictiveModeling)
data("GermanCredit")
set.seed(100)
inTrain=createDataPartition(GermanCredit$Class, p = 0.8)[[1]]
inTrain
GermanCreditTrain=GermanCredit[ inTrain, ]
GermanCreditTest=GermanCredit[-inTrain, ]
head(GermanCreditTrain)
head(GermanCreditTest)
set.seed(1056)
svmfit=train(Class~ .,data=GermanCreditTrain, method="svmRadial", preProc=c("center", "scale"), 
             tuneLength=10, 
             trControl=trainControl(method="repeatedcv", repeats=5, classProbs=TRUE))
svmfit
#first method: classification or regression model
#train control: the resampling method
#tuneLength: an integer denoting the amount of granularity in the tuning parameter grid
plot(svmfit, scales=list(x=list(log=2)))
predictedclasses=predict(svmfit, GermanCreditTest)
str(predictedclasses)
predictedprobs=predict(svmfit, newdata=GermanCreditTest, type="prob")
head(predictedprobs)
#between-model comparisons
#set.seed(1056)
#logisticreg=train(Class~ ., data=GermanCreditTrain, method="glm",
#            trcontrol=trainControl(method="repeatedcv", repeats=5))
#logisticreg
#resamp=resamples(list(SVM=svmfit, Logistic=logisticreg))
#summary(resamp)
#modeldifferences=diff(resamp)
#summary(modeldifference)

#kappa: sensitivity of output to changes or errors of input

Next week, I will continue to read the book.

Chapter 6.3 application

Today, I read Chapter 6 (6.3) and find something which could be useful for my research.

Summary

Partial Least Squares

The removal of highly correlated pairwise predictors may not guarantee a stable least squares solution. Alternatively, using PCA for pre-processing guarantees that the resulting predictors, or combinations thereof, will be uncorrelated.

Pre-processing predictors via PCA prior to performing regression in known as principal component regression (PCR).

If the variability in the predictor space is not related to the variability of the response, then PCR can have difficulty identifying a predictive relationship when one might actually exist. Because of this, it is recommended to use PLS when there are correlated predictors and a linear regression-type solution is desired.

While the PCA linear combinations are chosen to maximally summarize predictor space variability, the PLS linear combinations of predictors are chosen to maximally summarize covariance with the response. This means that PLS finds components that maximally summarize the variation of the predictors while simultaneously requiring these components to have maximum correlation with the response. (predictors-components-response)

PLS has one tuning parameter: the number of components to retain.

Tomorrow, I will continue to read the book.