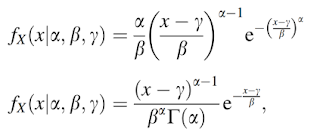Some functions for fitting

Today, I put data into Matlab and tried to find some functions useful for my research.

Summary:
T2distribution(:,1)=[]
T2distri=T2distribution
T2row1=T2distri(1,:)
T2row2=T2distri(2,:)
T2row3=T2distri(3,:)
T2row4=T2distri(4,:)
subplot(2,2,1)
area(T2row1)
subplot(2,2,2)
area(T2row2)
subplot(2,2,3)
area(T2row3)
subplot(2,2,4)
area(T2row4)

They are the first 4 distributions of T2. I just plot 4 of them to see how the distributions are like. They are mainly twomodals.

The following are two kind of fitting functions.

1.
General model Fourier3:
     f(x) =  a0 + a1*cos(x*w) + b1*sin(x*w) +
               a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w)
       where x is normalized by mean 32.5 and std 18.62
Coefficients (with 95% confidence bounds):
       a0 =   0.0007262  (0.0006442, 0.0008081)
       a1 =   0.0002028  (3.608e-05, 0.0003696)
       b1 =  -0.0009519  (-0.001061, -0.0008427)
       a2 =  -0.0006422  (-0.0007004, -0.000584)
       b2 =  -0.0003332  (-0.000459, -0.0002074)
       a3 =  -0.0001401  (-0.0002752, -4.879e-06)
       b3 =  -1.008e-05  (-5.636e-05, 3.62e-05)
       w =       1.857  (1.655, 2.059)

Goodness of fit:
  SSE: 9.065e-07
  R-square: 0.9812
  Adjusted R-square: 0.9789
  RMSE: 0.0001272

2.
General model Weibull:
     f(x) = a*b*x^(b-1)*exp(-a*x^b)
Coefficients (with 95% confidence bounds):
       a =    0.001374  (-0.0002114, 0.00296)
       b =      0.8532  (0.5792, 1.127)

Goodness of fit:
  SSE: 4.666e-05
  R-square: 0.03477
  Adjusted R-square: 0.0192
  RMSE: 0.0008675

As shown in the figure, the single Weibull is  not effective for fitting. In contrast, the Fourier of 3 terms is effective.

Tomorrow, I will continue to find more effective functions for fitting.

Modelling irregular and multimodal tree diameter distributions by FMM

Today, I read the paper 'Modelling irregular and multimodal tree diameter distributions by FMM'. It introduced an application of FMM to realistic problems. I think it is really helpful for my research. I sketched the logic of this whole method.

Summary:
There are a few steps to apply FMM to modelling irregular and multimodal tree diameter distributions:
1. select database as samples
2. select regular distributions

the upper one is Weibull distribution and the other is gamma distribution.
The finite mixture dnesity functions consisting of two or three Weibull distributions and two or three gamma distributions can be written as

the upper one is k=2 and the other is k=3.
3. use multistart method (MM) to choose initial parameter values (weights and components)
4. estimate the parameters of the mixture model using MLE
5. apply MLE by using EM algorithm with a Newton-type (NT) method to optimize the parameters
6. evaluate the fitting results by p value of chi-square test, bias and RMSE

I think they could be applied to my research.

Tomorrow, I will try to find corresponding codes in Matlab to realize the logic. There are many related packages in Matlab and I think I can find them in Matlab.

Some Papers and Books for Finite Mixture Models

Today, I first read the theoretical part of finite mixture models again and learnt a little more about it. Then, I tried to find some applications of finite mixture models to NMR T2 distribution, but there is little research on it. At last, I found something related to my research.

Summary:
These are what I found in the evening.There are two books and five papers. They are all related to finite mixture models. Some tell the theoretical part. Some tell the applications. I hope they will be helpful for my research and I will read them at the weekend.
I am trying to apply the methods to predict NMR T2 distribution now. But I have not found the best way to divide NMR T2 distribution to normal distributions. I will try to find it ASAP.

Tomorrow, I will read these books and papers carefully.

Expectation-maximization Algorithm

Today, I learned about the Expectation-maximization Algorithm.

Summary:
It is a method of iteration to get the best parameters for MLE.

Intuitively, this means that by maximizing in regard to a parameterization Θp-1, we obtain a parameterization Θp that maximizes the log likelihood. Based on this result, the EM algorithm works by iterating between two steps. In the first (E-step), it finds the expected value of the complete likelihood given the current parameterization Θp-1. In the second step (M-step), it looks for the set of parameters Θp that maximize the expectation from the E-step. At each iteration, the EM increases the log-likelihood converging to a local maximum. These steps are repeated P times or until a convergence criterion is fulfilled.

For now, I can only find the theoretical part of the method and I cannot find the examples or applications of them. As a result, it is difficult for me to apply the method. I will try to find details about examples and applications of the method ASAP.

Tomorrow, I will try to find examples of the methods so that I know how to apply the methods.

Finite Mixture Models

Today, I went on searching for mathematical solution. Finite Mixture Models may be helpful. They are combined with Maximum Likelihood Estimate.

Summary:

Finite Mixture Models

Pdf: probability density function

For a given data X with N observations, the likelihood of the data assuming that xi are independently distributed is given by

The problem of mixture estimation from data X can be formulated as to find the set of parameters Θ that gives the maximum likelihood estimate (MLE) solution

One way is to maximize the complete likelihood in an expectation-maximization (EM) approach.

Expectation-maximization Algorithm

The likelihood of the complete data (X; Y) takes the following multinomial form

where 1 is the indicator function, i.e. 1(yi = k) = 1 if yi = k holds, and 1(yi = k) = 0 otherwise.

There are some examples that I have not read. Today, I focused on the theoretical part.

Tomorrow, I will read more examples and try to associate them with my research.

 

Maximum Likelihood Estimate

Today, I found one method (MLE) that could be useful for my research.

Summary:
It is Maximum Likelihood Estimate (MLE).
It is about how to estimate one parameter so that the probability of our sample (NMR T2 distribution) happening could be the largest. The method can not make sure to predict NMR T2 distribution, it can just adjust parameters to make the probability to be the largest.
If it could be applied to NMR T2 distribution, the steps may be:
1. set parameters for normal and log-normal distributions;
2. build the estimating function;
3. solve the function;
4. obtain the best parameters;
5. estimate the errors and evaluate the results.

For now, I am trying to know how to build the estimating function with these parameters. I will try to set parameters reasonably so that it can be applied to this method.

Tomorrow, I will continue to learn about this method.

Divide T2 distribution

Today, I tried to figure out how to divide T2 distribution into 2 or 3 Gaussian or log-normal distributions.

Summary:
First, I looked into many distributions and found that normal and log-normal may be the most suitable ones. For example, Poisson distribution is more suitable for integers.
Both normal (Gaussian) and log-normal distributions have 2 parameters, namely miu and sigma. So one distribution includes two parameters. Today, I found that most papers said about how to add two or more distributions into one, but not dividing.
Later on, I found that Matlab can fit one distribution to one normal or log-normal distribution. However, it cannot fit one distribution to two or more normal and log-normal distributions. At least, I have not found it out.
Then, I tried to look for some papers about how to divide T2 distributions, but I have not found it out. Most papers just talk about how their models predict data well. One of the papers I read divided T2 distributions into 8 CMR Bin Porosity (CBP).  So the prediction of T2 distribution turned into the prediction of 8 CBPs. There are 4 models to be compared. Every CBP is predicted by 4 models and the paper found that CMIS (Committee machine with intelligent systems), which is  the combination of the other three models, performed the best.
I think that it is more reasonable to directly divide T2 distributions into 2 or 3 other distributions. The problem now is that I am not sure how to divide.

Tomorrow, I will continue to try to find how to divide T2 distributions into normal and log-normal distributions. 

Finish selecting data

Today, I read two papers and finished selecting parameters from Hess data.

It may be the final version of our parameters for our research. I think I have included all possible parameters into it.
I have sent it to you by email. It is in 6 edition sheet.

Next week, I will focus on how to divide NMR T2 distribution into 2 or 3 Gaussian or log-normal distribution and find the unknowns.

Apply data to R

Today, I reviewed R codes and started to apply the data to R.

I have sent you the data by email. If there is no problem, I will work on them.

I have done the depth matching. They are now can be applied to R without hesitation.

Tomorrow, I will continue to split the data and pre-process the data.

Deal with the data

Today, I changed the parameters as you said. Also, I added 4 new parameters to my data matrix. I tried to deal with the data so that they can be applied to R.

In addition, I have a question when I select more data today.

New parameters:

SonicScanner:DTCO

US/FT SonicScanner:DTSM US/FT

QElan:DPHZ

ft3/ft3 QElan:NPOR_EC ft3/ft3

I have collected all the parameters to IP software named NMRprediction. There are 23 parameters in total. 1 is depth and 1 is NMR permeability. So the total is 25.

Question:

What is the difference between QElan and RTscanner and Sonicscanner? They all include data from AT10 to AT90. I compared them and found that they almost have the same values. The difference is that QElan and RTscanner data depth range is from about 9000 ft to 11200 ft and Sonicscanner data depth range is from about 2000 ft to 11200 ft. For now, I selected AT10, AT60 and AT90 from Sonicscanner.

Tomorrow, I will continue to deal with the data and code.

Continue to select data and read the book

Today, I finished selecting data from Hess. In addition, I tried to find some papers and books about predicting NMR permeability and pore size distribution. I also read one of the book about NMR.

Parameters:

NMR_IP:nmrPerm

md GR EDTC gAPI Wire:DPHI_DOL ft3/ft3 Wire:DPHI_LIM ft3/ft3

Wire:DPHI_SAN

ft3/ft3 Wire:RVDRU ohm.m Wire:RVSRU ohm.m SonicScanner:AT10 OHMM SonicScanner:AT90 OHMM Core_SGR4:Kdsbu % Core_SGR4:THdsbu PPM Core_SGR4:Udsbu PPM Core_CT:Densitybuds gm/cc ELLAN2:BOUND_WATER_QEds v/v ELLAN2:CALCITE_QEds v/v ELLAN2:CHLORITE_QEds v/v ELLAN2:DOLOMITE_QEds v/v ELLAN2:HALITE_QEds v/v ELLAN2:ILLITE_QEds v/v ELLAN2:KEROGEN_QEds v/v ELLAN2:MONTMORILLONITE_QEds v/v ELLAN2:QUARTZ_QEds v/v ELLAN2:N-FELDSPAR_QEds v/v ELLAN2:K-FELDSPAR_QEds v/v Mdl1:Swu dec

(Do you have any recommendations of these parameters? should I delete or add some parameters else?)

Tomorrow, I will read books and papers about predicting NMR permeability and pore size distribution.

wu

Select Data

Today, I reviewed the data in IP and selected about 20 parameters from IP. I also did depth matching so that they can be applied to R as a total data matrix.

The data has been saved in Excel.

Tomorrow, I will continue to select parameters from IP. Once finished, I will start to use it in R.