NMR physics

Today, I reviewed the basic knowledge of NMR so that I would be able to find the proper predictors of it.

Summary

Data selection

No diaelectric data because they are also very expensive.

Try to use GR, neutron, sonic, density, resistivity data to predict NMR.

NMR:

NMR porosity is independent of matrix minerals, and the total response is very sensitive to fluid properties. Differences in relaxation times and/or fluid diffusivity allow NMR data to be used to differentiate clay-bound water, capillary-bound water, movable water, gas, light oil, and viscous oils. NMR-log data also provide information concerning pore size, permeability, hydrocarbon properties, vugs, fractures, and grain size.

T1: the longitudinal relaxation time.

T2: the transverse or spin-spin relaxation.

The decay or relaxation time of the NMR signals (T2) is directly related to the pore size. The NMR signal detected from a fluid-bearing rock therefore contains T2 components from every different pore size in the measured volume. Using a mathematical process known as inversion, these components can be extracted from the total NMR signal to form a T2 spectrum or T2 distribution, which is effectively a pore size distribution.

The so-called ‘T2 cut-off’ in a T2 distribution is the T2 value that divides the small pores that are unlikely to be producible from the larger pores that are likely to contain free fluid. The integral of the distribution above the T2 cut-off is a measure of the free fluid (mobile fluid) in the rock.  The portion of the curve below the cut-off is known as bound fluid and is made up of the clay bound fluid and the capillary bound fluid.

Tomorrow, I will continue to learn more about NMR and try to find the proper predictors.

Chapter 7 application (7.3&7.4)

Today, I finished Chapter 7 (7.3&7.4) and found something useful for my research.

Summary

SVM: Support Vector Machines

SVMs are a class of powerful, highly flexible modeling techniques.

The SVM regression coefficients minimize

There are several aspects of this equation worth pointing out. First, the use of the cost value effectively regularizes the model to help alleviate the over-parameterized problem. Second, the individual training set data points are required for new predictions. Only a subset of training set data points where , are needed for prediction. Since the regression line is determined using these samples, they are called the support vectors as they support the regression line. Which kernel function should be used? This depends on the problem. Note that some of the kernel functions have extra parameters. These parameters, along with the cost value, constitute the tuning parameters for the model.

K-Nearest Neighbors

Two commonly noted problems are computational time and the disconnect between local structure and the predictive ability of KNN.

Next week, I will continue to read the book and try to finish it before the holiday.

Chapter 7 application (7.2)

Today, I read Chapter 7 (7.2) and find something useful for my research.

Summary

MARS: Multivariate Adaptive Regression Splines

GCV: generalized cross-validation

There are two tuning parameters associated with the MARS model: the degree of the features that are added to the model and the number of retained terms. The latter parameter can be automatically determined using the default pruning procedure (using GCV), set by the user or determined using an external resampling technique.

There are several advantages to using MARS. First, the model automatically conducts feature selection; the model equation is independent of predictor variables that are not involved with any of the final model features. This point cannot be underrated. Given a large number of predictors seen in many problem domains, MARS potentially thins the predictor set using the same algorithm that builds the model. In this way, the feature selection routine has a direct connection to functional performance. The second advantage is interpretability. Each hinge feature is responsible for modeling a specific region in the predictor space using a (piecewise) linear model. When the MARS model is additive, the contribution of each predictor can be isolated without the need to consider the others. This can be used to provide clear interpretations of how each predictor relates to the outcome. For nonadditive models, the interpretive power of the model is not reduced. Finally, the MARS model requires very little pre-processing of the data; data transformations and the filtering of predictors are not needed.

Another method to help understand the nature of how the predictors affect the model is to quantify their importance to the model. For MARS, one technique for doing this is to track the reduction in the root mean squared error (as measured using the GCV statistic) that occurs when adding a particular feature to the model.

The following figure compares the predictors and we can see the importance of predictors from the figure.

Tomorrow, I will continue to read the book.

Chapter 7 application (7.1)

Today, I read Chapter 7 (7.1) to find something useful for my research.

Summary

Nonlinear Regression Models

Neural Networks

Weight decay is an approach to moderate over-fitting. It is a penalization method to regularize the model similar to ridge regression.

As the regularization value λ increases, the fitted model becomes more smooth and less likely to over-fit the training set.

Of course, the value of this parameter must be specified and, along with the number of hidden units, is a tuning parameter for the model. Reasonable values of λ range between 0 and 0.1. Also note that since the regression coefficients are being summed, they should be on the same scale; hence the predictors should
be centered and scaled prior to modeling.

Neural networks are models which are more accurate than linear models. It can be used to be applied to the log data. After building the data matrix, we may have dozens of predictors, namely log data to predict outcomes, namely NMR data. Before building the model , we can first center and scale predictors and use PCA to decrease correlations between every pair of predictors. Then we can set a set of tuning parameters of weight decay and number of hidden units to build the model. After running the codes, we can find the optimized tuning parameter so that  we can choose the optimized neural network model. It may perform well in predicting NMR data.

If we can just find the local optimization but not the global one, we can use the model averaged neural networks to solve the problem. The approach is that we start do modeling with several different starting numbers so that we can get different results of the model. Then we average them to get the more reliable results.

The following is an example of the comparison of neural networks with different tuning parameters.

Tomorrow, I will continue to read the book.

Chapter 6 Application (6.4&6.5)

Today, I finished reading Chapter 6 to find something useful for my research.

Summary

Because the dimension reduction offered by PLS is supervised by the response, it is more quickly steered towards the underlying relationship between the predictors and the response.

NIPALS: nonlinear iterative partial least squares algorithm

The constructs of NIPALS could be obtained by working with a “kernel” matrix of dimension P × P, the covariance matrix of the predictors (also of dimension P×P), and the covariance matrix of the predictors and response (of dimension P ×1). This adjustment improved the speed of the algorithm, especially as the number of observations became much larger than the number of predictors.

SIMPLS: simple modification of the PLS algorithm.

If a more intricate relationship between predictors and response exists, then we suggest employing one
of the other techniques rather than trying to improve the performance of PLS through this type of augmentation.

Partial least square regression vs. Ordinary least square regression

Penalized models

Combatting collinearity by using biased models may result in regression models where the overall MSE
is competitive.

One method of creating biased regression models is to add a penalty to the sum of the squared errors.

Ridge regression adds a penalty on the sum of the squared regression parameters:

Penalty increase, bias increase, variance decrease, model under-fit.

Lasso: least absolute shrinkage and selection operator model

A generalization of the lasso model is the elastic net. This model combines the two types of penalties:

The advantage of this model is that it enables effective regularization via the ridge-type penalty with the feature selection quality of the lasso penalty.

Tomorrow, I will continue to read Chapter 7 of the book.

Review of Codes

Today, I review the codes of the book from Chapter 3 to Chapter 5.

I think that I forget some of the codes when I read the book, so I decide to spend some time reviewing them.

Summary

#Coefficient of determination (R^2): the proportion of the information in the data that is explained by the model.
#It is a measure of correlation, not accuracy. It is dependent on the variation in the outcome. Same RMSE, larger variance, larger R^2.
observed=c(0.22, 0.83, -0.12, 0.89, -0.23, -1.30, -0.15, -1.4, 0.62, 0.99, -0.18, 0.32, 0.34,
           -0.3, 0.04, -0.87, 0.55, -1.3, -1.15, 0.2)
predicted=c(0.24, 0.78, -0.66, 0.53, 0.7, -0.75, -0.41, -0.43, 0.49, 0.79, -1.19, 0.06, 0.75,
           -0.07, 0.43, -0.42, -0.25, -0.64, -1.26, -0.07)
#in practice, the vector of predictions would be produced by the model function
residualvalues=observed-predicted
residualvalues
summary(residualvalues)
axisrange=extendrange(c(observed, predicted))
plot(observed, predicted, ylim=axisrange, xlim=axisrange)
abline(0, 1, col="darkgrey", lty=2)
plot(predicted, residualvalues, ylab = "residual")
abline(h=0, col="darkgrey", lty=2)
library(caret)
R2(predicted, observed)
RMSE(predicted, observed)
cor(predicted, observed)
cor(predicted, observed, method = "spearman")

library(AppliedPredictiveModeling)
data(twoClassData)
str(predictors)
str(classes)
set.seed(1)
library(caret)
trainingrows=createDataPartition(classes, p=0.8, list=FALSE)
head(trainingrows)
trainpredictors=predictors[trainingrows, ]
trainclasses=classes[trainingrows]
testpredictors=predictors[-trainingrows, ]
testclasses=classes[-trainingrows]
trainpredictors
trainclasses
testpredictors
testclasses
#maxdissim
#resampling
set.seed(1)
repeatedsplits=createDataPartition(trainclasses, p=0.8, time=3)
str(repeatedsplits)
#to create indicators for 10-fold cross-validation
set.seed(1)
cvsplits=createFolds(trainclasses, k=10, returnTrain = TRUE)
str(cvsplits)
fold1=cvsplits[[1]]
cvpredictors1=trainpredictors[fold1,]
cvclasses1=trainclasses[fold1]
nrow(trainpredictors)

nrow(cvpredictors1)

#e1071package contains the tune function
#errorest function in the ipred package
#the train function in the caret package
library(caret)
library(AppliedPredictiveModeling)
data("GermanCredit")
set.seed(100)
inTrain=createDataPartition(GermanCredit$Class, p = 0.8)[[1]]
inTrain
GermanCreditTrain=GermanCredit[ inTrain, ]
GermanCreditTest=GermanCredit[-inTrain, ]
head(GermanCreditTrain)
head(GermanCreditTest)
set.seed(1056)
svmfit=train(Class~ .,data=GermanCreditTrain, method="svmRadial", preProc=c("center", "scale"), 
             tuneLength=10, 
             trControl=trainControl(method="repeatedcv", repeats=5, classProbs=TRUE))
svmfit
#first method: classification or regression model
#train control: the resampling method
#tuneLength: an integer denoting the amount of granularity in the tuning parameter grid
plot(svmfit, scales=list(x=list(log=2)))
predictedclasses=predict(svmfit, GermanCreditTest)
str(predictedclasses)
predictedprobs=predict(svmfit, newdata=GermanCreditTest, type="prob")
head(predictedprobs)
#between-model comparisons
#set.seed(1056)
#logisticreg=train(Class~ ., data=GermanCreditTrain, method="glm",
#            trcontrol=trainControl(method="repeatedcv", repeats=5))
#logisticreg
#resamp=resamples(list(SVM=svmfit, Logistic=logisticreg))
#summary(resamp)
#modeldifferences=diff(resamp)
#summary(modeldifference)

#kappa: sensitivity of output to changes or errors of input

Next week, I will continue to read the book.

Chapter 6.3 application

Today, I read Chapter 6 (6.3) and find something which could be useful for my research.

Summary

Partial Least Squares

The removal of highly correlated pairwise predictors may not guarantee a stable least squares solution. Alternatively, using PCA for pre-processing guarantees that the resulting predictors, or combinations thereof, will be uncorrelated.

Pre-processing predictors via PCA prior to performing regression in known as principal component regression (PCR).

If the variability in the predictor space is not related to the variability of the response, then PCR can have difficulty identifying a predictive relationship when one might actually exist. Because of this, it is recommended to use PLS when there are correlated predictors and a linear regression-type solution is desired.

While the PCA linear combinations are chosen to maximally summarize predictor space variability, the PLS linear combinations of predictors are chosen to maximally summarize covariance with the response. This means that PLS finds components that maximally summarize the variation of the predictors while simultaneously requiring these components to have maximum correlation with the response. (predictors-components-response)

PLS has one tuning parameter: the number of components to retain.

Tomorrow, I will continue to read the book.

Chapter 5&6(6.1 6.2) application

Today, I read Chapter 5&6(6.1 6.2) to find something useful which could be used in my research.

Summary

Chapter 5 Application

Quantitative measures of performance

RMSE: the square root of MSE so that it is in the same units as the original data

: the proportion of the information in the data that is explained by the model. It is a measure of correlation, not accuracy.

The variance-bias trade-off: high variance or high bias, that is a question. Increasing bias can reduce model variance.

Chapter 6 Application

Ordinary linear regression finds parameter estimates that have minimum bias, whereas ridge regression, the lasso, and the elastic net find estimates that have lower variance.

Linear regression:

SSE: sum-of-squared errors.

When there are highly correlated predictors, we should remove one of the offending predictors or find models which can tolerate collinearity.

Tomorrow, I will read more of the book to frame questions.

Chapter 4 application

Today, I read Chapter 4 to find something which could be used in my research.

Summary

Over-fitting

Model tuning: tune an appropriate value of a tuning parameter

Data splitting: maximum dissimilarity sampling

Common steps in model building:

1.      Pre-processing the predictor data

2.      Estimating model parameters

3.      Selecting predictors for the model

4.      Evaluating model performance

5.      Fine tuning class prediction rules (via ROC curves, etc)

Resampling techniques:

1.      K-fold cross validation

2.      Generalized cross validation (approximate the leave-one-out error rate)

For example, in the last leave-one-out cross validation, df=1 and n=12.

3.      Repeated training/testing splits

4.      Bootstrap

Choose final tuning parameters with different considerations of various factors

Choosing between models:
1. Start with several models that are the least interpretable and most flexible.

2. investigate simpler models that are less opaque

3. consider using simplest model that reasonably approximates the performance of the more complex methods

Chapter 3 application 2

Today, I finished reading chapter 3 and found something which could be applied to my research. In addition, I looked into IP to try to know what do all the data mean. I have known some of them basically.

Summary

Tomorrow, I will read chapter 4 to find more information which may be useful for my research.

Chapter 3 application

Today, I browsed the rest of the paper and started to look into the data. There are many ways of data pre-processing in chapter 3 and they can be applied into the log data.

Summary

paper:

Chapter 3:

1. Individual predictors:

Centering: the predictor has a zero mean

Scaling: each value of the predictor variable is divided by its standard deviation. Scaling the data coerce the values to have a common standard deviation of one.

Removing skewness: Box-Cox transformation

After holiday, I will start to frame questions of each chapter and try to apply them into the data.

Preparing for using data

Today, I started to look into data in IP and tried to be familiar with IP software. Also, Yifu gave me a paper which is written by the people from Hess Corporation. I read a little of it.

Summary

SPWLA paper

TOC: total organic carbon

According the paper, the lithology is very complicated. I think if I need to predict NMR permeability with R method, the lithology of the data and the lithology of where I need to predict should be similar.

Tomorrow, I will continue to read the paper and look into the data.

Chapter 10 (Computing finished)

Today, I fixed some problems of computing of Chapter 10.

Codes:
pp2=preProcess(age28data[, 1:7], "pca")
pca1=predict(pp2, age28data[, 1:7])
head(pca1)
pca1$Data="Training Set"
pca1$Data[startpoints]="Starting Values"
pca3=predict(pp2, cbresults[, 1:7])
pca3$Data="Cubist"
head(pca3)
pca4=predict(pp2, nnetresults[, 1:7])
pca4$Data="Neural Network"
head(pca4)
pcadata=rbind(pca1, pca3, pca4)
dim(pcadata)
pcadata$Data=factor(pcadata$Data,
                    levels = c("Training Set","Starting Values",
                    "Cubist","Neural Network"))
lim=extendrange(pcadata[, 1:2])

# convert a vector of strings into a vector of numbers
m=with(pcadata, as.numeric(levels(factor(as.numeric(factor(pcadata$Data))))))
m=with(pcadata, levels(factor(Data)))
m
colm=c()
for(i in 1:length(pcadata$Data))
{
  colm[i]=which(pcadata$Data[i]==m)
}
colm

xyplot(PC2 ~ PC1, data = pcadata, groups = Data,
       auto.key = list(columns = 2),
       xlim = lim, ylim = lim,
       col=colm,
       type = c("g", "p")
      )

xyplot(PC2 ~ PC1, data = pcadata, groups = Data,
       auto.key = list(columns = 2),
       xlim = lim, ylim = lim,
       col=c("blue", "pink", "red", "green"),
       type = c("g", "p")
)

Next week, I will start to look into the NMR data.

Chapter 10 computing

Today, I did computing of Chapter 10.

Codes:
modelPrediction=function(x, mod)
{
  if(x[1] < 0 | x[1] > 1) return(10^38)
  if(x[2] < 0 | x[2] > 1) return(10^38)
  if(x[3] < 0 | x[3] > 1) return(10^38)
  if(x[4] < 0 | x[4] > 1) return(10^38)
  if(x[5] < 0 | x[5] > 1) return(10^38)
  if(x[6] < 0 | x[6] > 1) return(10^38)
  x=c(x, 1 - sum(x))
  if(x[7] < 0.05) return(10^38)
  tmp <- as.data.frame(t(x))
  names(tmp)=c('Cement','BlastFurnaceSlag','FlyAsh',
               'Superplasticizer','CoarseAggregate',
               'FineAggregate', 'Water')
  tmp$Age=28
  -predict(mod, tmp)
}

# Cubist mdoel
cbresults=startingvalues
cbresults$Water=NA
cbresults$Prediction=NA
cbresults
for(i in 1:nrow(cbresults))
{
  results=optim(unlist(cbresults[i,1:6]),
                     modelPrediction,
                     method = "Nelder-Mead",
                    control=list(maxit=5000),
                      mod = cbmodel)
  cbresults$Prediction[i]=-results$value
  # save the final mixture values
  cbresults[i,1:6]=results$par
}
#col.sums <- apply(x, 2, sum)  row.sums <- apply(x, 1, sum)  rbind  cbind
cbresults$Water=1 - apply(cbresults[,1:6], 1, sum)
# Keep the top three mixtures, -: decreasing order
cbresults=cbresults[order(-cbresults$Prediction),][1:3,]
cbresults$Model="Cubist"
cbresults

       Cement BlastFurnaceSlag      FlyAsh Superplasticizer CoarseAggregate FineAggregate      Water Prediction  Model
523 0.1747206       0.17969922 0.012880890     0.0027363548       0.3200175     0.2532112 0.05673427  102.44370 Cubist
495 0.2098331       0.05295034 0.006751067     0.0003692619       0.3538669     0.3238973 0.05233208   86.01767 Cubist
477 0.2110388       0.04514574 0.062017524     0.0023323792       0.3178446     0.3077021 0.05391885   85.51025 Cubist

# neural network model
nnetresults=startingvalues
nnetresults$Water=NA
nnetresults$Prediction=NA
nnetresults
for(i in 1:nrow(nnetresults))
{
  results=optim(unlist(nnetresults[i,1:6]),
                modelPrediction,
                method = "Nelder-Mead",
                control=list(maxit=5000),
                mod = nnetmodel)
  nnetresults$Prediction[i]=-results$value
  nnetresults[i,1:6]=results$par
}
nnetresults$Water=1 - apply(nnetresults[,1:6], 1, sum)
nnetresults=nnetresults[order(-nnetresults$Prediction),][1:3,]
nnetresults$Model="NNet"
nnetresults

       Cement BlastFurnaceSlag       FlyAsh Superplasticizer CoarseAggregate FineAggregate      Water Prediction Model
69  0.1617514       0.13291706 5.509921e-10      0.007644831       0.3905959     0.2564540 0.05063673   81.92797  NNet
357 0.1366392       0.04989215 2.395829e-08      0.002012726       0.4513948     0.3012054 0.05885566   80.16362  NNet
477 0.2145572       0.04306283 4.614330e-02      0.001330241       0.2993219     0.3299018 0.06568276   79.59500  NNet
(I am faced with some problems of drawing graphs. Tomorrow, I will try to fix them.)

Tomorrow, I will fix some problems of the codes.

Chapter 10 computing

Today, I continued to do computing of Chapter 10.

Codes:
# plot the RMSE values
parallelplot(allresamples)
# using R2
parallelplot(allresamples, metric="Rsquared")

nnetpredictions=predict(nnetmodel, testset)
gbmpredictions=predict(gbmmodel, testset)
cbpredictions=predict(cbmodel, testset)

age28data=subset(trainingset, Age==28)
dim(age28data)
# remove the age and compressive strength columns and
# then center and scale the predictor columns
pp1=preProcess(age28data[,-(8:9)], c("center", "scale"))
scaledtrain=predict(pp1, age28data[, 1:7])
dim(scaledtrain)
# a single random mixture is selected to initialize the maximum dissimilarity sampling process
set.seed(91)
startmixture=sample(1:nrow(age28data), 1)
starters=scaledtrain[startmixture, 1:7]
#select 14 more mixtures to complete a diverse set of starting points for the search algorithms
library(proxy)
maxdis=maxDissim(starters, scaledtrain, 14)
maxdis
startpoints=c(startmixture, maxdis)
starters=age28data[startpoints, 1:7]
starters
# all seven mixture proportions should add to one
# the water proportion will be determined by the sum of the other six ingredient proportions
# remove water
startingvalues=starters[, -4]

Tomorrow, I will continue to do computing of Chapter 10.

Chapter 10 computing

Today, I did computing of Chapter 10.

Codes:
library(AppliedPredictiveModeling)
data(concrete)
str(concrete)
str(mixtures)
library(Hmisc)
library(caret)
# g: grid; p: points; smooth: smoother between: add space between panels.
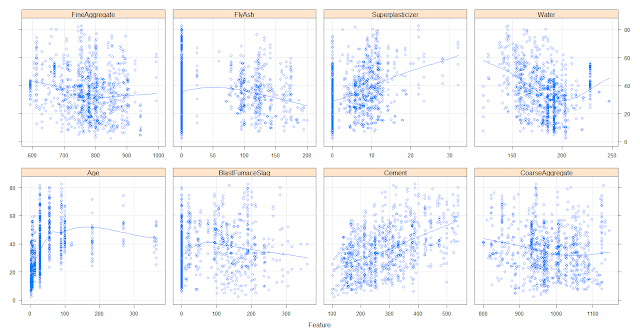
featurePlot(x=concrete[,-9], y=concrete$CompressiveStrength,
            between=list(x=1, y=1),
            type=c("g", "p", "smooth"))
# ? averaging the replicated mixtures and splitting the data into training and test sets
library(plyr)
averaged=ddply(mixtures, .(Cement, BlastFurnaceSlag, FlyAsh, Water, Superplasticizer, CoarseAggregate,
                           FineAggregate, Age), function(x) c(CompressiveStrength=mean(x$CompressiveStrength)))
str(averaged)
set.seed(975)
fortraining=createDataPartition(averaged$CompressiveStrength, p=3/4)[[1]]
trainingset=averaged[fortraining,]
testset=averaged[-fortraining,]
dim(trainingset)
dim(testset)
# The dot in the formula below is shorthand for all predictors and
# (.)^2 expands into a model with all the linear terms and all two-factor interactions.
modformula=paste("CompressiveStrength ~ (.)^2 + I(Cement^2) + ",
                 "I(BlastFurnaceSlag^2)+I(FlyAsh^2)+I(Water^2)+",
                 "I(Superplasticizer^2)+I(CoarseAggregate^2)+",
                 "I(FineAggregate^2)+I(Age^2)")
modformula=as.formula(modformula)
modformula
# the predictors' number of modformula is different from the book, but after the test of a different one, modformula2,
modformula2=paste("CompressiveStrength ~ (.)^2")
modformula2=as.formula(modformula2)
modformula2
# modformula and modformula2 have different results of linearreg although their predictors' numbers are the same.
# so I guess that modformula is correct.
controlobject=trainControl(method="repeatedcv", repeats=5, number=10)
set.seed(669)
linearreg=train(modformula, data=trainingset, method="lm", trControl=controlobject)
linearreg

# the other two linear models were created
set.seed(669)
plsmodel=train(modformula, data=trainingset, method="pls", preProcess = c("center", "scale"),
               tuneLength = 15, trControl = controlobject)
plsmodel
# centered (44) and scaled (44): 44 is right.
library(elasticnet)
enetgrid2=expand.grid(.lambda=c(0, 0.001, 0.01, 0.1),
                      .fraction=seq(0.05, 1, length=20))
set.seed(669)
enetmodel2=train(modformula, data=trainingset, method="enet", preProcess = c("center", "scale"),
                 tuneGrid=enetgrid2, trControl=controlobject)
enetmodel2

# MARS
library(earth)
set.seed(669)
earthmodel=train(CompressiveStrength~., data=trainingset, method="earth",
                 tuneGrid=expand.grid(.degree=1, .nprune=2:25), trControl=controlobject)
earthmodel

#SVMs
library(kernlab)
set.seed(669)
svmmodel=train(CompressiveStrength~., data=trainingset, method="svmRadial",
               tuneLength=15, preProcess=c("center", "scale"), trControl=controlobject)
svmmodel

# Neural Networks
library(nnet)
nnetgrid=expand.grid(.decay=c(0.001, 0.01, 0.1), .size=seq(1, 27, by=2), .bag=FALSE)
set.seed(669)
nnetmodel=train(CompressiveStrength~., data=trainingset, method="avNNet",
                tuneGrid=nnetgrid, preProcess=c("center", "scale"),
                linout=TRUE, trace=FALSE, maxit=1000, trControl=controlobject)
nnetmodel

# regression and model trees
library(rpart)
set.seed(669)
rpartmodel=train(CompressiveStrength~., data=trainingset, method="rpart",
                 tuneLength=30, trControl=controlobject)
rpartmodel

set.seed(669)
library(party)
ctreemodel=train(CompressiveStrength~., data=trainingset, method="ctree",
                 tuneLength=10, trControl=controlobject)
ctreemodel

set.seed(669)
library(RWeka)
mtmodel=train(CompressiveStrength~., data=trainingset, method="M5",
              trControl=controlobject)
mtmodel

# remaining model objects
library(ipred)
library(plyr)
library(e1071)
set.seed(669)
treebagmodel=train(CompressiveStrength~., data=trainingset, method="treebag",
                   trControl=controlobject)
treebagmodel

library(randomForest)
set.seed(669)
rfmodel=train(CompressiveStrength~., data=trainingset, method="rf",
              tuneLength=7, ntrees=1000, importance=TRUE,
              trControl=controlobject)
rfmodel

gbmgrid=expand.grid(.interaction.depth = seq(1, 7, by = 2),
                    .n.trees = seq(100, 1000, by = 50),
                    .shrinkage = c(0.01, 0.1), .n.minobsinnode=10)
library(gbm)
set.seed(669)
gbmmodel=train(CompressiveStrength~., data=trainingset, method="gbm",
               tuneGrid=gbmgrid, verbose=FALSE, trControl=controlobject)
gbmmodel

cubistgrid=expand.grid(.committees = c(1, 5, 10, 50, 75, 100),
                       .neighbors = c(0, 1, 3, 5, 7, 9))
library(Cubist)
set.seed(669)
cbmodel=train(CompressiveStrength~., data=trainingset, method="cubist",
              tuneGrid=cubistgrid, trControl=controlobject)
cbmodel
allresamples=resamples(list("Linear Reg"=lmmodel), "PLS"=plsmodel,
                       "Elastic Net"=enetmodel2, "MARS"=earthmodel,
                       "SVM"=svmmodel,
                       # "Neural Networks"=nnetmodel,
                       "CART"=rpartmodel, "Cond Inf Tree" = ctreemodel,
                       "Bagged Tree" = treebagmodel, "Boosted Tree" = gbmmodel,
                       "Random Forest" = rfmodel, "Cubist" = cbmodel))
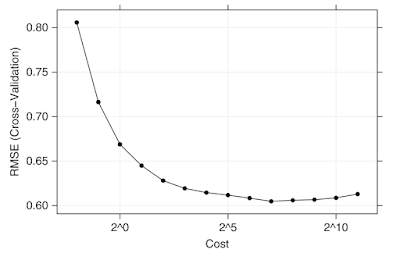
(There should be a figure of comparison among these models. However, the nnetmodel takes so much time to calculate that it has not shown the result till now. I will keep it calculating all the night and it should show the result tomorrow.)

Tomorrow, I will continue to do computing of Chapter 10.

Chapter 10 (10.1 10.2 10.3)

Today, I read Chapter 10 (10.1 10.2 10.3) and started to do computing of Chapter 10.

Summary

Case Study: Compressive Strength of Concrete Mixtures

A balanced design is one where no one experimental factor (i.e., the predictors) has more focus than the others. In most cases, this means that each predictor has the same number of possible levels and that the frequencies of the levels are equivalent for each factor.

Sequential experimentation

1.     Screen a large number of possible experimental factors to determine important factors

2.     More focused experiments are created with subset of important factors

3.     The nature of relationship between the important factors can be further elucidated

4.     Fine-tune a small number of important factors

In this chapter, models will be created to help find potential recipes to maximize compressive strength.

Model Building Strategy

A data splitting approach will be taken for this case study. A random holdout set of 25 % (n = 247) will be used as a test set and five repeats of 10-fold cross-validation will be used to tune the various models。

Model Performance

The top performing models were tree ensembles (random forest and boosting), rule ensembles (Cubist), and neural networks.

Optimizing Compressive Strength

Many rely on determining the gradient (i.e., first derivative) of the prediction equation. Several of the models have smooth prediction equations (e.g., neural networks and SVMs).

Neural networks: smooth model

Cubist: non-smooth model

Computing

library(AppliedPredictiveModeling)

data(concrete)

str(concrete)

str(mixtures)

library(Hmisc)

library(caret)

# g: grid; p: points; smooth: smoother between: add space between panels.

featurePlot(x=concrete[,-9], y=concrete$CompressiveStrength,

            between=list(x=1, y=1),

            type=c("g", "p", "smooth"))

#averaging the replicated mixtures and splitting the data into training and test sets

library(plyr)

averaged=ddply(mixtures, .(Cement, BlastFurnaceSlag, FlyAsh, Water, Superplasticizer, CoarseAggregate,

                           FineAggregate, Age), function(x) c(CompressiveStrength=mean(x$CompressiveStrength)))

str(averaged)

set.seed(975)

fortraining=createDataPartition(averaged$CompressiveStrength, p=3/4)[[1]]

trainingset=averaged[fortraining,]

testset=averaged[-fortraining,]

Tomorrow, I will continue to do computing of Chapter 10.

Chapter 9

Today, I read Chapter 9.

Summary

A Summary of Solubility Models

With the exception of poorly performing models, there is a fairly high correlation between the results derived from resampling and the test set (0.9 for the RMSE and 0.88 for R2).

There was a “pack” of models that showed better results, including model trees, linear regression, penalized linear models, MARS, and neural networks.

The group of high-performance models include support vector machines (SVMs), boosted trees, random forests, and Cubist.

There are very few statistically significant differences among high-performance models. Given this, any of these models would be a reasonable choice.

Next week, I will read Chapter 10, which is the last chapter of Part 2 of the book. After finishing Chapter 10, I think it is time to apply them into the real data.

Chapter 8 Exercises

Today, I finished exercises of Chapter 8.

# 8.5
library(caret)
data(tecator)
absorp
# moisture fat protein
endpoints
absorpchange=absorp
dim(absorpchange)
absorpchange2=cbind(absorpchange, moisture=endpoints[,1])
absorpchange2=data.frame(absorpchange2)
library(RWeka)
treemodel1=M5P(moisture~., data=absorpchange2)
plot(treemodel1)

set.seed(100)
treemodel2=train(absorpchange2[,1:100], absorpchange2$moisture, method="M5", trControl = trainControl(method = "cv"),
             control= Weka_control(M=10))
treemodel2 # RMSE min = 6.5
plot(treemodel2)
toohigh=findCorrelation(cor(absorpchange2[,1:100]), cutoff = 0.999)
toohigh
trainabsorp=absorpchange2[,-toohigh]
treemodel3=M5P(moisture~., data=trainabsorp)
plot(treemodel3)

set.seed(100)
treemodel4=train(trainabsorp[,1:4], trainabsorp$moisture, method="M5", trControl = trainControl(method = "cv"),
                 control= Weka_control(M=10))
treemodel4 # RMSE min = 6.0
plot(treemodel4)

 

# 8.6
library(AppliedPredictiveModeling)
data(permeability)
dim(fingerprints)
permeability
library(caret)
lowfrequencies=nearZeroVar(fingerprints, freqCut = 20, uniqueCut = 10)
fingerfiltered=fingerprints[, -lowfrequencies]
dim(fingerfiltered)
library(randomForest)
rfmodel=randomForest(permeability~., data=fingerfiltered)
plot(rfmodel)
rfmodel2=randomForest(fingerfiltered, permeability, importance = TRUE, ntrees=1000)
plot(rfmodel2)
imp=importance(rfmodel2)
# %IncMSE: the higher number, the more important
# IncNodePurity: More useful variables achieve higher increases in node purities

Tomorrow, I will read Chapter 9.