Chapter 10 (10.1 10.2 10.3)

Today, I read Chapter 10 (10.1 10.2 10.3) and started to do computing of Chapter 10.

Summary

Case Study: Compressive Strength of Concrete Mixtures

A balanced design is one where no one experimental factor (i.e., the predictors) has more focus than the others. In most cases, this means that each predictor has the same number of possible levels and that the frequencies of the levels are equivalent for each factor.

Sequential experimentation

1.     Screen a large number of possible experimental factors to determine important factors

2.     More focused experiments are created with subset of important factors

3.     The nature of relationship between the important factors can be further elucidated

4.     Fine-tune a small number of important factors

In this chapter, models will be created to help find potential recipes to maximize compressive strength.

Model Building Strategy

A data splitting approach will be taken for this case study. A random holdout set of 25 % (n = 247) will be used as a test set and five repeats of 10-fold cross-validation will be used to tune the various models。

Model Performance

The top performing models were tree ensembles (random forest and boosting), rule ensembles (Cubist), and neural networks.

Optimizing Compressive Strength

Many rely on determining the gradient (i.e., first derivative) of the prediction equation. Several of the models have smooth prediction equations (e.g., neural networks and SVMs).

Neural networks: smooth model

Cubist: non-smooth model

Computing

library(AppliedPredictiveModeling)

data(concrete)

str(concrete)

str(mixtures)

library(Hmisc)

library(caret)

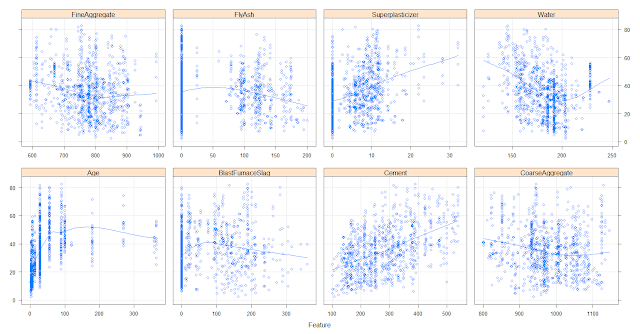
# g: grid; p: points; smooth: smoother between: add space between panels.

featurePlot(x=concrete[,-9], y=concrete$CompressiveStrength,

            between=list(x=1, y=1),

            type=c("g", "p", "smooth"))

#averaging the replicated mixtures and splitting the data into training and test sets

library(plyr)

averaged=ddply(mixtures, .(Cement, BlastFurnaceSlag, FlyAsh, Water, Superplasticizer, CoarseAggregate,

                           FineAggregate, Age), function(x) c(CompressiveStrength=mean(x$CompressiveStrength)))

str(averaged)

set.seed(975)

fortraining=createDataPartition(averaged$CompressiveStrength, p=3/4)[[1]]

trainingset=averaged[fortraining,]

testset=averaged[-fortraining,]

Tomorrow, I will continue to do computing of Chapter 10.