2 new SVM models

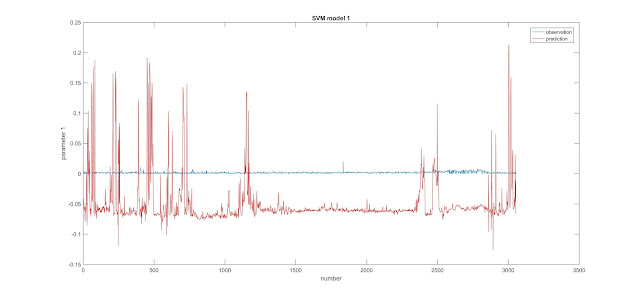
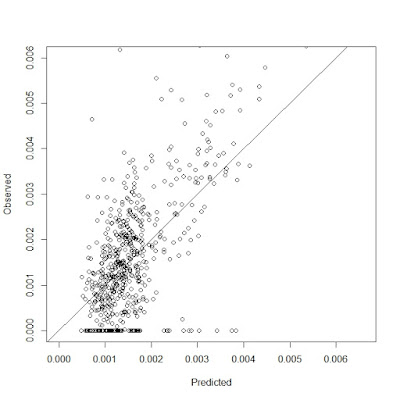
Today, I learned how to build SVM models and built 2 SVM models.

Summary;

first model:

second model:

The first figures for both models are outputs of the regression with the minimum estimated cross-validation loss.
The second figures for both models are comparison of observation values and prediction values, which do not show good results.

Tomorrow, I will try to improve the models to get better results.

try ANN and SVM models for logging data and T2 parameters

Today, I tried ANN and SVM again.

Summary:

ANN:

SVM:

svmstd =

  RegressionSVM
             ResponseName: 'Y'
    CategoricalPredictors: []
        ResponseTransform: 'none'
                    Alpha: [1104×1 double]
                     Bias: 0.0015
         KernelParameters: [1×1 struct]
                       Mu: [1×16 double]
                    Sigma: [1×16 double]
          NumObservations: 3055
           BoxConstraints: [3055×1 double]
          ConvergenceInfo: [1×1 struct]
          IsSupportVector: [3055×1 logical]
                   Solver: 'SMO'

The result is like that. The model converged after 552 iterations.
The MSE of the model is 1.1725e-6.

The model is not good enough yet. There may be two reasons.
First, for ANN, 3055 observations with 16 predictors may not be big enough to build a good model. The data matrix is not big enough. So ANN is not suitable for building the model.
Second, We should delete some noises of logging data manually.

Tomorrow, I will continue to apply it to SVM and verify two assumptions mentioned above.

try several models

Today, I tried several models. They include Cubist, Random Forest and SVM. But after trials and errors, I could not find that they have good modeling results.

Summary:

SVM:

 Random Forest:

Cubist:

All of their R2 are lower than 0.5, which show bad modeling results.

Yesterday's ANN flow chart:

I find that there are also some packages of ANN and other models in Matlab. 

Next week, I plan to look into them to find if they can be helpful for my research.

Draw a flow chart for ANN and draw the ANN prediction results

Today, I draw a flow chart for ANN and draw the ANN prediction results, which is not good.

Summary:

I sent you a ppt file to show the flow chart of how to build an ANN model.

The following is the bad behavior of this ANN model.

Y is our data. X is predicted data. They should be near the line (y=x).

Tomorrow, I will try to improve the model or find another better model to predict our data.

Start to apply logging data and parameter matrix in R

Today, I started to apply logging data and parameter matrix in R.

Summary:

I try to select 6 most possible models to predict:

ANN, Boosted tree, Cubist, Random forest, SVM and Elastic Net.

As what I read last semester, these six are the best ones used to predict other kinds of data.

At this evening, I code for ANN model. Now the laptop is calculating and it has not finished yet. So I do not know if it is good or not for now. I will leave it calculating by itself. Tomorrow, I may get some results.

Codes:

## T2 Prediction

head(betapredict)

head(logmatch)

betaorigin=betapredict

logorigin=logmatch

logchange1=logorigin

betachange1=betaorigin

library(caret)

set.seed(1)

trainingrows=createDataPartition((1:3055), p=0.8, list=FALSE)

head(trainingrows)

trainlog=logchange1[trainingrows, ]

trainbeta=betachange1[trainingrows,]

testlog=logchange1[-trainingrows, ]

testbeta=betachange1[-trainingrows,]

library(earth)

library(kernlab)

library(nnet)

library(MASS)

parameter1=trainbeta$P1

parameter2=trainbeta$P2

parameter3=trainbeta$P3

parameter4=trainbeta$P4

parameter5=trainbeta$P5

parameter6=trainbeta$P6

ctr1=trainControl(method = "cv", number = 10)

nnetgrid=expand.grid(.decay=c(0, 0.01, 0.1), .size=c(1:10), .bag=FALSE)

set.seed(100)

nnettune=train(trainlog, parameter1, method="avNNet", tuneGrid = nnetgrid, trControl = ctr1,

               preProcess = c("center", "scale"), linout = TRUE, trace = FALSE, 

               MaxNWts = 10*(ncol(trainlog)+1)+10+1, maxit=200)

nnettune

Tomorrow, I will continue to build models and compare them.

Results：

Model Averaged Neural Network 

2447 samples
  16 predictor

Pre-processing: centered (16), scaled (16) 
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 2202, 2202, 2202, 2201, 2202, 2203, ... 
Resampling results across tuning parameters:

  decay  size  RMSE         Rsquared 
  0.00    1    0.001182810  0.2659956
  0.00    2    0.001178855  0.2652559
  0.00    3    0.001176240  0.2700417
  0.00    4    0.001171193  0.2758881
  0.00    5    0.001171282  0.2757166
  0.00    6    0.001175032  0.2719288
  0.00    7    0.001169831  0.2771893
  0.00    8    0.001170633  0.2768607
  0.00    9    0.001173294  0.2730265
  0.00   10    0.001174102  0.2723126
  0.01    1    0.001202662  0.2380567
  0.01    2    0.001202690  0.2380329
  0.01    3    0.001202191  0.2388848
  0.01    4    0.001201014  0.2403814
  0.01    5    0.001208686  0.2342891
  0.01    6    0.001192577  0.2520885
  0.01    7    0.001187736  0.2564749
  0.01    8    0.001188651  0.2550046
  0.01    9    0.001189708  0.2548316
  0.01   10    0.001190979  0.2544052
  0.10    1    0.001212622  0.2285682
  0.10    2    0.001211344  0.2293782
  0.10    3    0.001209365  0.2291870
  0.10    4    0.001211336  0.2291943
  0.10    5    0.001211175  0.2295812
  0.10    6    0.001204673  0.2362646
  0.10    7    0.001203994  0.2369177
  0.10    8    0.001202633  0.2369342
  0.10    9    0.001203141  0.2373625
  0.10   10    0.001204911  0.2364219

Tuning parameter 'bag' was held constant at a value of FALSE
RMSE was used to select the optimal model using  the smallest value.


The final values used for the model were size = 7, decay = 0 and bag = FALSE. 

The results come out now but R2 of training model is not very good. The largest is smaller than 0.3. It should be at least 0.7. I will try to figure it out today.

Change x-axis from bins to t2 in ms and recalculate R2

Today, I changed x-axis from bins to t2 in ms and recalculated R2.

Summary:
After ignoring the first several or last several points with large residuals, I improved most of the low R2 depths.

There are only 11 depths with R2 lower than 0.7 and 3 depths with R2 lower than 0.4. The lowest is 0.293 (the middle one of the second figure). I think the reason is not only for the first or last peaks but also for the bad fitting results in middle parts, which is unavoidable for this fitting functions if I need the accuracy for other depths.

The following is the new R2 distributions for all used 3055 depths.

Tomorrow, I will do depth matching for logging data and parameters data and start applying them in R.

Depth shifting and find poor fitting results

Today, I drew figures for logging data of depth shifting and found the poor fitting results.

Summary:

First, I search online and find the explanation for R2 to be negative.

R2 compares the fit of the chosen model with that of a horizontal straight line (the null hypothesis). If the chosen model fits worse than a horizontal line, then R2 is negative. Note that R2 is not always the square of anything, so it can have a negative value without violating any rules of math. R2 is negative only when the chosen model does not follow the trend of the data, so fits worse than a horizontal line.

A negative R2 is not a mathematical impossibility or the sign of a computer bug. It simply means that the chosen model (with its constraints) fits the data really poorly.

Second, I make sure that all the logging data I use are depth shifted.

Third, I found the fitting depths whose R2 is lower than 0.7 and 0.

There are 154 depths whose R2 are lower than 0.7. There are 26 depths whose R2 are lower than 0.

The first plot is for the first 16 dpeths lower than 0.7 and the second and third are for lower than 0.

I think although the values of 0.7 and 0 are very different, the fitting plots are similar. They all cannot fit the first declining curves or the last ascending curves.

For the last 5th small picture, it does not fit any peaks, which shows bugs in my code. After fixing bugs, There are 151 depths whose R2 are lower than 0.7. There are 25 depths whose R2 are lower than 0.

The first plot is for the first 25 depths lower than 0.7 and the second is for lower than 0.

Now the smallest R2 (about -0.4) depth is deleted automatically.

After adjusting for several times, the percentages of each category are shown as follows (3 means 3 or more).

Tomorrow, I will start to apply these data into R.

fix one problem

Today, I fixed one problem, which was that my codes could not identify peaks if they have two or more largest values of one peak. They are now solved.

Summary:

The above are the new first 32 depths used to be fitted.

As a result, their fitting results are better than yesterday's.

The following is the new R2 distribution.

Next week, I will start to predict the parameters of these distributions with some models.

fit T2 distribution

Today, I fitted T2 distribution with adjusted guassian distributions.

Summary:

Most of the fitting results are very good shown in the figures.

The R^2 distribution figure shows that most of them are close to 1, which means that  the fitting results are very good. However, there are some very small R^2. It is obvious that these fitting has problems.

These are the first 16 depths to be fitted. Most of them are really good. Most of their R2 is larger than 0.9. However, some of them are not good.
For example, the 16th figure showed a bad fitting result. The reason is that: the largest peak of the 16th figure has three largest values, which are equal to each other. As a result, My code cannot identify that this is a peak. Also, maybe there are some other problems before fitting.

I will try to solve the problem tomorrow and see if there are any other questions.

adjust all the depth

Today, I discussed with you, Dr. Misra, and made an agreement about how to deal with the imperfect data. Finally, I have keep all depths following the agreement.

Summary:

I conclude all depths' conditions of t2 distribution and made a sheet (3 means 3 or more).

Codes changed:

%% whole depth
% find peaks
for i=1:4256
    for j=2:63
        if T2distri(i,j-1)<T2distri(i,j) && T2distri(i,j)>T2distri(i,j+1)
            p(i,j)=T2distri(i,j);
        end
    end
end

[row,col,v]=find(p);
col1=col+1;
p2=[row,col1,v]; % ascending it by row
% if there are more than two peaks at one depth, delete some of them

p3=p2;

for i=1:9674
    if p3(i,1)==p3(i+1,1) && p3(i+1,1)==p3(i+2,1)
        if p3(i,3)>=0.1*p3(i+1,3) && p3(i,3)>=0.1*p3(i+2,3) && p3(i+1,3)>=0.1*p3(i,3) && p3(i+1,3)>=0.1*p3(i+2,3) &&  p3(i+2,3)>=0.1*p3(i,3) && p3(i+2,3)>=0.1*p3(i+1,3)                  
        p3(i,3)=0;
        p3(i+1,3)=0;
        p3(i+2,3)=0;
        end
    end
end

for i=1:9675
    if p3(i,3)==0
        if p3(i,1)==p3(i+1,1)
           p3(i+1,3)=0;
        end
    end
end

for i=1:6046 % change till the end
    if p3(i,3)==0
        p3(i,:)=[];
    end
end
% for every depth with more than 2 peaks and other peaks cannot be ignored,
% i have deleted them.

p4=p3;

%% for other depths with more than 2 peaks, i can choose the largest 2 peaks
for i=1:5651 % change till the end
    if p4(i,1)==p4(i+1,1) && p4(i+1,1)==p4(i+2,1)
        if p4(i,3)<p4(i+1,3) && p4(i,3)<p4(i+2,3)
            p4(i,:)=[];
        else if p4(i+1,3)<p4(i,3) && p4(i+1,3)<p4(i+2,3)
            p4(i+1,:)=[];
            else
               p4(i+2,:)=[];
            end
        end
    end
end
% now there is only one or two peaks at every depth


%% adjust two peaks at every depth
p5=p4;

for i=2:6175 % change the number till the end
    if p5(i,1)~=p5(i-1,1) && p5(i,1)~=p5(i+1,1)
        if p5(i,2)<=32          
        p5=[p5(1:i,:);[p5(i,1),0,0];p5(i+1:end,:)];
        else
        p5=[p5(1:i-1,:);[p5(i,1),0,0];p5(i:end,:)];
        end
    end
end

%% set initial values for iteration
for i=1:6176  
    if p5(i,3)==0
        beta0(i,:)=[0;0;0];
    else
        beta0(i,:)=[0.01;1;p5(i,3)];
    end      
end

I have set the initial values for iteration for every depth.

Tomorrow, I will do the fitting step.

fit T2 distribution with gaussian distributions at every depth 1

Today, I tried to fit T2 distribution with gaussian distributions at every depth.

Summary:
1. I  find peaks at every depth. But there are 1 or 2 or 3 or more peaks at some depth. Some of them are really small though.
2. If there are more than 2 peaks at one depth, I decide to delete some of them and keep two peaks at most.
3. If there are only 1 peak at one depth, I copy it so that every depth has two peaks.
4. I also find that there are no peaks at some depth. I finally find that it is because the shape of T2 distribution at some depth are like this:

So I add the first and last point value to data matrix as the peaks at some depth.
5. Finally there are two peaks at every depth.
6. I set initial values for iteration when fitting. Because there may cause calculating problems when fitting in Matlab if the initial values are not similar to the results. So setting initial values for iteration is very important.

The following are codes I write today.

%% whole depth
% find peaks
for i=1:4256
    for j=2:63
        if T2distri(i,j-1)<T2distri(i,j) && T2distri(i,j)>T2distri(i,j+1)
            p(i,j)=T2distri(i,j);
        end
    end
end

[row,col,v]=find(p);
col1=col+1;
p2=[row,col1,v]; % ascending it by row
% if there are more than two peaks at one depth, delete some of them
p3=p2;

for i=1:7977 % change the number till the end
    if p3(i,1)==p3(i+1,1) && p3(i+1,1)==p3(i+2,1)
        if p3(i,3)<p3(i+1,3) && p3(i,3)<p3(i+2,3)
            p3(i,:)=[];
        else if p3(i+1,3)<p3(i,3) && p3(i+1,3)<p3(i+2,3)
                p3(i+1,:)=[];
            else
                 p3(i+2,:)=[];
            end
        end
    end
end
% now there is only one or two peaks at every depth

%% adjust two peaks at every depth
p4=p3;
for i=2:8483 % change the number till the end
    if p4(i,1)~=p4(i-1,1) && p4(i,1)~=p4(i+1,1)
        p4=[p4(1:i,:);p4(i,:);p4(i+1:end,:)];
    end
end
% but there are some missing depth

%% add missing depth
p5=p4;
for i=2:8512
    if p5(i,1)>=p5(i-1,1)+2
        p5=[p5(1:i-1,:);[p5(i-1,1)+1,1,T2distri(p5(i-1,1)+1,1)];
            [p5(i-1,1)+1,64,T2distri(p5(i-1,1)+1,64)];p5(i:end,:)];
    end
end

%% set initial values for iteration
for i=1:8512,
    beta0(i,:)=[0.01;1;p5(i,3)];
end

Tomorrow, I will try to finish the following part of fitting T2 distribution at every depth.

Fit T2 distribution with 2 gaussian distributions

Today, I successfully fitted T2 distribution with 2 gaussian distributions.

Summary:

%% fit T2 with gaussian distribution
% b(1) is scale, b(2) is sigma, b(3) is miu.
modelfun1=@(b,x)(b(1)*(1/(b(2)*sqrt(2 * pi))) * exp(-(x - b(3)).^2 ./ (2 * b(2)^2)));
x1=(1:40);
y1=T2row1(:,(1:40));
x2=(40:64);
y2=T2row1(:,(40:64));
beta10=[0.01;1;10];
beta20=[0.01;1;50];
beta1=nlinfit(x1,y1,modelfun1,beta10);
beta2=nlinfit(x2,y2,modelfun1,beta20);
[beta1,R1,J1,CovB1,MSE1,ErrorModelInfo1]=nlinfit(x1,y1,modelfun1,beta10);
[beta2,R2,J2,CovB2,MSE2,ErrorModelInfo2]=nlinfit(x2,y2,modelfun1,beta20);
fun1=beta1(1,:)*(1/(beta1(2,:)*sqrt(2 * pi))) * exp(-(x1 - beta1(3,:)).^2 ./ (2 * beta1(2,:)^2));
fun2=beta2(1,:)*(1/(beta2(2,:)*sqrt(2 * pi))) * exp(-(x2 - beta2(3,:)).^2 ./ (2 * beta2(2,:)^2));

%% plot
hold off;
plot(T2row1)
hold on;
plot(x1,fun1, 'r-');
plot(x2,fun2, 'r-');
title('T2 distribution fitting');
rsq1=1-sum(R1.^2)/sum((y1-mean(y1)).^2)
rsq2=1-sum(R2.^2)/sum((y2-mean(y2)).^2)

Result:

beta1 =

    0.0426
    6.5562
   19.3092

beta2 =

    0.0042
    2.6393
   49.9026

The first is the scale to adjust gaussian distribution, the second is standard deviation, the third is mean value. I calculated that the r square for the first gaussian distribution is 0.9695 and  the r square for the second gaussian distribution is 0.9907. Both of them are good enough for fitting.

Next week, I will try to apply the method to all the depth of T2 distribution.

Fitting T2 distribution may be a problem.

Today, I found that the prediction of T2 distribution may be unrealistic.

Summary:

The x-axis of T2 distribution is location such as 1, 2, 3, 4…… the y-axis of T2 distribution is the value that we want to predict.

If we want to fit T2 distribution with some other distributions, we should first know what these distributions are. Usually, we use the probability density function of distributions. The x-axis of some distribution is the values and the y-axis of it is the probability. So they are different from T2 distribution.

From Hess data, we know that there are 64 values in one specific depth. So the x-axis of T2 distribution is 1 to 64. The y-axis of T2 distribution is the value we want. Assuming that the 5^th and the 20^th value are the same, so they have the same y-value in T2 distribution figure. However, when we use the 64 data to do distribution fitting, the two values are regarded as the same one. They would both have the same x-axis value in the distribution and they contribute to the value’s probability as y-axis. As a result, the distribution we predict is totally different as the T2 distribution.

Tomorrow, I want to have a meeting with you if you have time.

GMM example

Today, I continued to look for FMM codes. Finally, I found one of GMM example. I think it is really helpful for fitting T2 distribution.

Summary:

First, I want to point out one problem:

In distribution, the pdf shows that y is the probability and x is the value of the variable. But in T2 distribution, the y is the value of T2 and x is just the time.

I will try to solve it.

 % $Author: ChrisMcCormick $    $Date: 2014/05/19 22:00:00 $    $Revision: 1.3 $

%%======================================================

%% STEP 1a: Generate data from two 1D distributions.

mu1 = 10;      % Mean

sigma1 = 1;    % Sigma

m1 = 100;      % Number of points

mu2 = 20;

sigma2 = 3;

m2 = 200;

% Generate the data.

X1 = (randn(m1, 1) * sigma1) + mu1;

X2 = (randn(m2, 1) * sigma2) + mu2;

X = [X1; X2];

%%=====================================================

%% STEP 1b: Plot the data points and their pdfs.

x = [0:0.1:30];

y1 = gaussian1D(x, mu1, sigma1);

y2 = gaussian1D(x, mu2, sigma2);

hold off;

plot(x, y1, 'b-');

hold on;

plot(x, y2, 'r-');

plot(X1, zeros(size(X1)), 'bx', 'markersize', 10);

plot(X2, zeros(size(X2)), 'rx', 'markersize', 10);

set(gcf,'color','white') % White background for the figure.

%%====================================================

%% STEP 2: Choose initial values for the parameters.

% Set 'm' to the number of data points.

m = size(X, 1);

% Set 'k' to the number of clusters to find.

k = 2;

% Randomly select k data points to serve as the means.

indeces = randperm(m);

mu = zeros(1, k);

for (i = 1 : k)

    mu(i) = X(indeces(i));

end

% Use the overal variance of the dataset as the initial variance for each cluster.

sigma = ones(1, k) * sqrt(var(X));

% Assign equal prior probabilities to each cluster.

phi = ones(1, k) * (1 / k)

%%===================================================

%% STEP 3: Run Expectation Maximization

% Matrix to hold the probability that each data point belongs to each cluster.

% One row per data point, one column per cluster.

W = zeros(m, k);

% Loop until convergence.

for (iter = 1:1000)

    

    fprintf('  EM Iteration %d\n', iter);

    %%===============================================

    %% STEP 3a: Expectation

    %

    % Calculate the probability for each data point for each distribution.

    

    % Matrix to hold the pdf value for each every data point for every cluster.

    % One row per data point, one column per cluster.

    pdf = zeros(m, k);

    

    % For each cluster...

    for (j = 1 : k)

        

        % Evaluate the Gaussian for all data points for cluster 'j'.

        pdf(:, j) = gaussian1D(X, mu(j), sigma(j));

    end

    

    % Multiply each pdf value by the prior probability for each cluster.

    %    pdf  [m  x  k]

    %    phi  [1  x  k]   

    %  pdf_w  [m  x  k]

    pdf_w = bsxfun(@times, pdf, phi);

    

    % Divide the weighted probabilities by the sum of weighted probabilities for each cluster.

    %   sum(pdf_w, 2) -- sum over the clusters.

    W = bsxfun(@rdivide, pdf_w, sum(pdf_w, 2));

    

    %%===============================================

    %% STEP 3b: Maximization

    %%

    %% Calculate the probability for each data point for each distribution.

    % Store the previous means so we can check for convergence.

    prevMu = mu;    

    

    % For each of the clusters...

    for (j = 1 : k)

    

        % Calculate the prior probability for cluster 'j'.

        phi(j) = mean(W(:, j));

        

        % Calculate the new mean for cluster 'j' by taking the weighted

        % average of *all* data points.

        mu(j) = weightedAverage(W(:, j), X);

    

        % Calculate the variance for cluster 'j' by taking the weighted

        % average of the squared differences from the mean for all data

        % points.

        variance = weightedAverage(W(:, j), (X - mu(j)).^2);

        

        % Calculate sigma by taking the square root of the variance.

        sigma(j) = sqrt(variance);

    end

    

    % Check for convergence.

    % Comparing floating point values for equality is generally a bad idea, but

    % it seems to be working fine.

    if (mu == prevMu)

        break

    end

% End of Expectation Maximization loop.    

end

%%=====================================================

%% STEP 4: Plot the data points and their estimated pdfs.

x = [0:0.1:30];

y1 = gaussian1D(x, mu(1), sigma(1));

y2 = gaussian1D(x, mu(2), sigma(2));

% Plot over the existing figure, using black lines for the estimated pdfs.

plot(x, y1, 'k-');

plot(x, y2, 'k-');

I think it is the most suitable example close to my research.

Tomorrow, I will continue to look into it.

EM algorithm for GMM applied in Matlab

Today, I finished reading the paper and  found codes for fitting a Gaussian Mixture Model to data.

Summary:

Models in the paper:

Weibull distribution

Log-normal distribution

Generalized gamma distribution

Generalized F-distribution

Use a mixture of parametric distributions

A mixture of two gamma distributions

Codes:
options = statset('Display','final');
gm = fitgmdist((T2row1)',2,'Options',options);

ComponentMeans = gm.mu
ComponentCovariances = gm.Sigma
MixtureProportions = gm.PComponents

AIC = zeros(1,4);
gm = cell(1,4);
for k = 1:4
    gm{k} = fitgmdist(X,k);
    AIC(k)= gm{k}.AIC;
end

[minAIC,numComponents] = min(AIC);
numComponents

gm2 = gm{numComponents}

I applied the codes to the first row of NMR T2 distribution data and get the following results:

30 iterations, log-likelihood = 391.441

ComponentMeans =

    0.0002
    0.0018


ComponentCovariances(:,:,1) =

   4.7465e-08


ComponentCovariances(:,:,2) =

   3.3443e-07


MixtureProportions =

    0.6682    0.3318


numComponents =

     2


gm2 =

Gaussian mixture distribution with 2 components in 2 dimensions
Component 1:
Mixing proportion: 0.500000
Mean:   -3.0377   -4.9859

Component 2:
Mixing proportion: 0.500000
Mean:    0.9812    2.0563

There are only codes for plotting the contour figures instead of fitting codes.

Tomorrow, I will continue to learn how to plot fitting figures and improve the fitting results.

Estimating the cure fraction in population-based cancer studies by using FMM

Today, I read the paper 'Estimating the cure fraction in population-based cancer studies by using FMM'. The estimating result shown in the paper was good. I will try to understand all of them and see if models in this paper can be applied in my research.

Summary:
The cure fraction (the proportion of patients who are cured of disease) is of interest
to both patients and clinicians and is a useful measure to monitor trends in survival of curable
disease. The paper extends the non-mixture and mixture cure fraction models to estimate the
proportion cured of disease in population-based cancer studies by incorporating a finite mixture
of two Weibull distributions to provide more flexibility in the shape of the estimated relative survival or excess mortality functions. The methods are illustrated by using public use data from
England and Wales on survival following diagnosis of cancer of the colon where interest lies
in differences between age and deprivation groups. We show that the finite mixture approach
leads to improved model fit and estimates of the cure fraction that are closer to the empirical
estimates.This is particularly so in the oldest age group where the cure fraction is notably lower.
The cure fraction is broadly similar in each deprivation group, but the median survival of the
‘uncured’ is lower in the more deprived groups. The finite mixture approach overcomes some of
the limitations of the more simplistic cure models and has the potential to model the complex
excess hazard functions that are seen in real data. 

The estimating result is shown below, which is good.

Tomorrow, I will look more into the paper.

Looking for best functions for fitting T2 distribution

Today, I continue to looking for the best functions for fitting T2 distribution.

Summary:
T2distribution(:,1)=[];
T2distri=T2distribution;
T2row1=T2distri(1,:);
T2row2=T2distri(2,:);
T2row3=T2distri(3,:);
T2row4=T2distri(4,:);

subplot(2,2,1)
area(T2row1)
subplot(2,2,2)
area(T2row2)
subplot(2,2,3)
area(T2row3)
subplot(2,2,4)
area(T2row4)

[phat1,pci1]=mle(T2row1,'distribution','gam')
[phat2,pci2]=mle(T2row2,'distribution','gam')
[phat3,pci3]=mle(T2row3,'distribution','gam')
[phat4,pci4]=mle(T2row4,'distribution','gam')

%% same as above
[phat1,pci1]=gamfit(T2row1)
[phat2,pci2]=gamfit(T2row2)
[phat3,pci3]=gamfit(T2row3)
[phat4,pci4]=gamfit(T2row4)
phat11=phat1(:,1);
phat12=phat1(:,2);
y1=gampdf(T2row1,phat11,phat12);
plot(y1)

[phat5,pci5]=mle(T2row1,'distribution','norm')
[phat6,pci6]=mle(T2row2,'distribution','norm')
[phat7,pci7]=mle(T2row3,'distribution','norm')
[phat8,pci8]=mle(T2row4,'distribution','norm')
phat51=phat5(:,1);
phat52=phat5(:,2);
y5=normpdf(T2row1,phat51,phat52);
plot(y5)

%% example
x = gaminv((0.005:0.01:0.995),100,10);
y = gampdf(x,100,10);
y1 = normpdf(x,1000,100);
figure;
plot(x,y,'-',x,y1,'-.')

After fitting, the results are not good. They are not even on the same order of magnitudes. I will try to solve the problem tomorrow.

Maximum Likelihood Estimates

Today, I looked into the application of MLE.

Summary:

function [theta] = LG_RML(u,y,oa,ob,od)
na = oa - 1;nb = ob - 1;nc = od - 1;d = 1;
L = length(u);
nn = max(na,nc);
uk = zeros(d + nb,1);
yk = zeros(na,1);
vk = zeros(nc,1);
yfk = zeros(nn,1);ufk = zeros(nn,1);vfk = zeros(nc,1);
thetae_1 = zeros(na+nb+1+nc,1);
thetae = zeros(na+nb+1+nc,L);
P = eye(na+nb+1+nc);
for k = 1:L
    hk = [-yk;uk(d:d+nb);vk];
    v = y(k) - hk'*thetae_1;
    hkf=[-yfk(1:na);ufk(d:d+nb);vfk];
    K=P*hkf/(1+hkf'*P*hkf);
    thetae(:,k)=thetae_1+K*v;
    P=( eye(na+nb+1+nc)-K*hkf' )*P;
    yf=y(k)-thetae(na+nb+2:na+nb+1+nc,k)*yfk(1:nc);%yf(k)
    uf=u(k)-thetae(na+nb+2:na+nb+1+nc,k)*ufk(1:nc);%uf(k)
    vf=v-thetae(na+nb+2:na+nb+1+nc,k)*vfk(1:nc);%vf(k)
    thetae_1=thetae(:,k);      
    for i=d+nb:-1:2
        uk(i)=uk(i-1);
    end
    uk(1)=u(k);    
    for i=na:-1:2
        yk(i)=yk(i-1);
    end
    yk(1)=y(k);
    for i=nc:-1:2
        vk(i)=vk(i-1);
        vfk(i)=vfk(i-1);
    end
    vk(1)=v;
    vfk(1)=vf;
    for i=nn:-1:2
        yfk(i)=yfk(i-1);
        ufk(i)=ufk(i-1);
    end
    yfk(1)=yf;
    ufk(1)=uf;
end
theta = thetae;
end

a=[1 -1.5 0.7];b=[1 0.5];c=[1 -0.5];d=1;
L=1000;
na=length(a)-1;nb=length(b)-1;nc=length(c)-1;
uk=zeros(d+nb,1);
yk=zeros(na,1);
u=randn(L,1);
xi=randn(L,1);
xik=zeros(nc,1);
for k=1:L
    y(k)=-a(2:na+1)*yk+b *uk(d:d+nb)+c *[xi(k);xik];
    for i=d+nb:-1:2
        uk(i)=uk(i-1);
    end
    uk(1)=u(k);
    for i=na:-1:2
        yk(i)=yk(i-1);
    end
    yk(1)=y(k);
    xik(1)=xi(k);
end
thetae = LG_RML(u,y,3,2,2);
figure(1)
plot([1:L],thetae(1:na,:),[1:L],thetae(na+nb+2:na+nb+1+nc,:));
xlabel(k);ylabel('parameter estimation a&d');
legend('a_1' ,'a_2' ,'d_1' );axis([0 L -2 2]);
figure(2)
plot([1:L],thetae(na+1:na+nb+1,:));
xlabel(k);ylabel('parameter estimation b' );
legend('b_0' ,'b_1' );axis([0 L 0 1.5]);

There are many applications of MLE. I will try to find one that is the most similar to my research.

Tomorrow, I will look more into MLE.